Применение понятия бесконечность в математике.

 

      Высказаться по этому поводу меня подтолкнуло письмо Марины Олеговны Ипатьевой с просьбой ответить на на тест из 3-х вопросов.

     До 1870 г. отношение к понятию бесконечности и бесконечным множествам было осторожным. Бесконечное множество считалось потенциальным. То есть к нему всегда можно добавить новый член, а построение его полностью не возможно. С 1870г. начали появляться работы Георга Кантора, который начал обращаться с бесконечными множествами как с законченными построениями. Такой подход ввёл понятие - актуальное бесконечное множество (построение которого законченно). Тогда появилась возможность приписывать бесконечным множествам свойства, которые ранее были для них недоступны. Например, определять счётное ли бесконечное множество или несчётное. Какое бесконечное множество имеет большую мощность, а какое меньшую и т.д. Постепенно в математике появилось отдельное направление - анализ бесконечных множеств. Можно подумать, что современники с восторгом приняли работы Георга Кантора. Это совсем не так. Теория Кантора первоначально была воспринята настолько нелогичной, парадоксальной и даже шокирующей, что натолкнулась на резкую критику со стороны математиков-современников, в частности, Анри Пуанкаре, Леопольда Кронекера. Позднее — Лёйтзена Брауэра и Германа Вейля, а Людвиг Витгенштейн высказал возражения философского плана.

     Идеи Кантора оказались столь неожиданными и противоречащими интуиции, что знаменитый французский математик Анри Пуанкаре назвал эти идеи «тяжёлой болезнью», от которой математика должна когда-нибудь излечиться.

     Учитель Кантора - Леопольд Кронекер, один из самых авторитетных математиков Германии — даже нападал на Кантора лично, называя его «научным шарлатаном», «ренегатом» и «растлителем молодежи».

     Витгенштейн с горечью отмечал, что математика «истоптана вдоль и поперёк разрушительными идиомами теории множеств», которое он отклоняет как «шутовство», «смехотворное» и «ошибочное».

     Критике противостояли одобрение и всемирная известность. В 1904 году Лондонское королевское общество наградило Кантора Медалью Сильвестра, высшей наградой, которую оно могло пожаловать. Сам Кантор верил в то, что теория трансфинитных чисел была сообщена ему свыше. Давид Гильберт, защищая теорию от критики, смело заявил: «Никто не изгонит нас из рая, который основал Кантор».

     Судьба Георга Кантора печальна. Известно, что Кантор был подвержен «нервным заболеваниям», участившимся с возрастом и всё более ослаблявшим его. Эти расстройства были, по-видимому, симптомами болезни мозга. Георг Кантор умер 6 января 1918 года в Галле, после продолжительного психического расстройства.

     Со временем противники теории Кантора ушли из жизни, а сама теория стала общепринятой. Но и в настоящее время у этой теории есть противники. Например, Валдис Валевич Эгле и его ученица и продолжательница его дела Марина Олеговна Ипатьева. Валдис Валевич занимался разработкой теории построения искусственного интеллекта, названный им Веданской теорией. И именно с этой позиции теория Кантора вызывает большие сомнения. С проектом Марины Олеговны можно познакомиться здесь.

     У меня к теории бесконечных множеств скептическое отношение. Попытаюсь изложить причины своего скепсиса.

 

 

     Возьмем бесконечный ряд натуральных чисел 1, 2, 3, 4 … ∞ и обозначим его, например а. Теперь выделим из а другой бесконечный ряд натуральных чисел – например, каждое пятое число, начиная с 1 - 1, 6, 11, 16 … ∞ и обозначим его как а₁ . Выделим ещё бесконечные ряды чисел с шагом 5, начинающихся с 2, 3, 4 и 5. Полученные бесконечные ряды чисел обозначим:                            а₂   2, 7, 12, 17 … ∞

                                                 а₃   3, 8, 13, 18 … ∞

                            а₄   4, 9, 14, 19 … ∞

                            а₅   5, 10, 15, 20 … ∞

 

(В принципе можно из бесконечного ряда натуральных чисел а выделить любое количество бесконечных рядов с неповторяющимися числами, вплоть до бесконечности, но остановимся на выбранном.)

 

     Так как ряды чисел а₁ , а₂ , а₃ , а₄ , а₅ бесконечны, то мы можем установить взаимно однозначное соответствие всех членов бесконечностей (по отдельности) с членами бесконечности а. А это значит, что бесконечности равны между собой.

а = а₁ = а₂ = а₃ = а₄ = а₅         (1)

 

     Теперь вспомним, что бесконечность а состоит из бесконечностей а₁ , а₂ , а₃ , а₄ , а₅ , так как числа бесконечностей а₁ , а₂ , а₃ , а₄ , а₅ не повторяются между собой, и используют все числа бесконечной последовательности а. Тогда мы можем составить уравнение:

а = а₁ + а₂ + а₃ + а₄ + а₅      (2)

или другое уравнение:

а - а₁ - а₂ - а₃ - а₄ - а₅ = 0      (3)

      А теперь помня выражение (1) попробуем подставить любое число (натуральное, дробное и т.д.) в выражение (2) и (3). Равенства мы не получим. Какой вывод можно сделать? То, что бесконечность нельзя выразить каким-либо числом, так как число всегда конечно. Что же нам это даёт? А то, что мы не в праве применять к понятию бесконечности, то что мы применяем к числам. Бесконечность – это отдельный класс объектов. Выражения (1), (2) и (3) показывают, что к бесконечности не применимо сложение и вычитание. Не применимы и другие действия с числами, как например деление, умножение и т.д. Нельзя также сравнивать бесконечности, и определять, что больше, что меньше. Так как всё что мы сравниваем и ставим знак >, < или = мы можем выразить числом. Мы не можем даже применять строгую математическую логику, так как мы её применяем к числам, или к тому, что можем выразить числом. Делая какие–либо манипуляции с числами бесконечного ряда, мы не можем делать ни какого вывода о самой бесконечности, так как она числом не является, и к ней какие-либо свойства числа не применимы.

     Может быть, всё-таки какие-то свойства чисел или конечных множеств, применимы к понятию бесконечности? Возможно, но это сначала надо доказать. Без этого доказательства мы вводим постулат о том, что свойства чисел или конечных множеств применимы к понятию бесконечности. А такой постулат совсем не очевиден. Этот постулат можно разделить на отдельные пункты по действиям, которые мы себе позволяем к бесконечным рядам чисел. Например, постулат о том, что к бесконечным рядам применимы понятия счётные – несчётные.

     Посчитать бесконечные ряды чисел можно разными методами. Самый простой – это когда числа следуют друг за другом. Если их разместить в виде какой-либо матрицы, то можно разработать различные алгоритмы для их подсчёта. Диагональный метод показывает, что не все бесконечные множества можно посчитать. Можно выделить условия (постулаты), при которых диагональный метод правилен. Что при других условиях (постулатах) он не правилен. Но тут не решается главная задача – применимо ли к бесконечным множествам свойства счётные – несчётные. Применимость не доказана, но общепринята. Для проверки данного утверждения попробуем при одинаковых постулатах получить совсем разные выводы.

 

Для примера возьмём доказательство диагональным методом с сайта:

http://ega-math.narod.ru/Singh/Cantor.htm (взят произвольно), и небольшой комментарий, взятый оттуда же (выделен цветом).

 

 

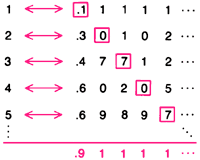
     Множество действительных чисел, представленное континуумом точек на прямой, не является счётным. Если бы оно было счётным, то действительные числа, скажем между 0 и 1, можно было бы одно за другим объединить в пары с целыми числами. Всякое действительное число в перечне можно представить бесконечным десятичным разложением (такие бесконечные десятичные дроби, как 0,5000..., представим в виде эквивалентной бесконечной дроби 0,4999...). Каков бы ни был перечень таких десятичных дробей, можно построить новую десятичную дробь, которая определяет некоторое действительное число и не содержится в этом перечне. Для этого на первом месте после запятой пишем 9, если первая цифра десятичного разложения первого действительного числа в перечне равна 1; в противном случае пишем 1. Аналогично изменяем вторую десятичную цифру во втором действительном числе, третью десятичную цифру в третьем и т.д. Построенное десятичное разложение представляет некоторое действительное число, расположенное между 0 и 1, но оно должно отличаться по крайней мере одним десятичным знаком от каждого действительного числа, входящего в перечень. Следовательно, предположение, что действительные числа можно объединить в пары с целыми числами, приводит к противоречию, а потому должно быть отброшено. Это доказательство основано на методе, называемом диагональным.

     Итак, будем считать, что при данных постулатах, процессом сопоставления действительных чисел промежутка 0 и 1 и целыми числами промежутка 1 и ∞ (назовём это процессом 1), доказана невозможность подсчёта целыми числами действительных чисел промежутка 0 и 1. Результаты сопоставления у нас записаны столбиком, и числа следуют друг за другом от верха к низу. Что же нам мешает запустить процесс 2, цель которого просто посчитать количество строчек результата сопоставления процесса 1? В любой момент остановки процесса 1 и нахождении несопоставимого действительного числа, процесс 2 посчитает натуральными числами весь столбик, вместе с несопоставимым числом. Мы можем сделать процесс 1 бесконечным. Для этого модифицируем процесс 1. Он будет выполнять процесс сопоставления, потом в какой-то момент останавливаться и находить несопоставимое действительное число. После чего продолжать диагональный процесс до следующей остановки, и поиска нового несопоставимого числа, и т.д. до бесконечности. Все результаты процесса 1 у нас размещены столбиком. Этот столбик мы можем продолжать до бесконечности. (Так как в этот столбик мы помещаем действительные числа промежутка 0 и 1, которые мы можем сопоставить с целыми числами 1 → ∞, а также не сопоставимые, то диагональ разрывается и смещается. От этого немного страдает наглядность, но суть дела не меняется. Мы можем, после того как записали число несопоставимое, дальше продолжить процесс сопоставления.)

 

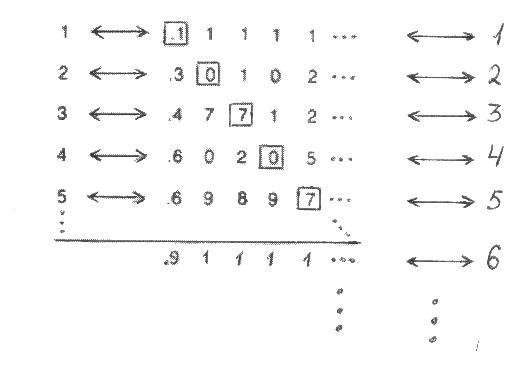
     Так как натуральных чисел у нас бесконечное множество, то мы можем сопоставить все строчки результата бесконечного процесса 1 целым числам 1→ ∞ . Что же получилось? При одинаковых постулатах, сначала мы показываем, что невозможно посчитать целыми числами промежутка 1 → ∞ действительные числа промежутка 0 → 1, а потом простым действием всё-таки считаем.

 

     Я считаю, что к бесконечным множествам понятия счётное – несчётное применять нельзя. Понятия счетные – несчётные, применяемые к бесконечным множествам, позволяют сравнивать их между собой, и утверждать какие бесконечные множества имеют большую мощность, какие меньшую, а какие одинаковую мощность. Если понятия счётные – несчётные к бесконечным множествам неприменимы, то и сравнивать между собой их нельзя. (Вспомним выражения (1), (2), (3).)

 

 

 Главная страница                                   Математика