Масса и энергия
Акимов И.Ю. Пятый постулат Евклида
Постулаты Евклида.
Допустим:
1.Что от всякой точки до всякой точки <можно> провести прямую линию.
2.И что ограниченную прямую <можно> непрерывно продолжать по прямой.
3.И что из всякого центра и всяким раствором <может быть> описан круг.
4.(Акс. 10.) И что все прямые углы равны между собой.
5.(Акс. 11.) И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные эти две прямые неограниченно встретятся с той стороны, где углы меньшие двух прямых.
(В статье используются «Начала Евклида» ОГИЗ 1948г. Перевод с греческого и комментарии Д.Д.Мордухай-Болтовского. В приложении 1 даны определения, аксиомы, постулаты и формулировки первых 29 предложений из данного издания.)
Так возможно ли доказать 5-й постулат? Сам постулат не удобен для доказательства. Но исследования в этом направлении выявили ряд утверждений, эквивалентных пятому постулату. То есть, если принять эти утверждения, то можно доказать 5-й постулат. Но и эти утверждения можно доказать, только приняв 5-й постулат.
На мой взгляд, самым удобным для доказательства эквивалентом 5-го постулата является утверждение: внутренние углы треугольника вместе равны двум прямым. В книге Евклида это утверждение включено в предложение 32. То есть после того, как применён 5-й постулат в предложении 29. Чтобы подчеркнуть, что мы не собираемся применять 5 постулат, и так как разрешим использовать предложения с 1-го по 26-е, назовём это утверждение предложением 26А.
Здесь и далее в статье будем указывать определения, аксиомы, постулаты и предложения, на которые будем опираться в доказательствах. Это делается не из любви к аксиоматическому методу. А для того, чтобы случайно не использовать то, что мы и пытаемся доказать.
Предложение 26А. Внутренние углы треугольника вместе равны двум прямым.
Доказательство.
Возьмём произвольный треугольник ABC. Стороны треугольника непрерывно продолжим по прямой (Постулат 2).
В точке A образуются четыре угла, а именно: EAB, BAC, CAD и DAE. Углы EAB и BAC вместе равны двум прямым (Предложение 13). Углы CAD и DAE вместе равны двум прямым (Предложение 13). Следовательно, четыре угла, образованные в точке A, вместе равны четырём прямым. Аналогично доказывается, что в точках B и C четыре угла, образованные в этих точках, вместе равны четырём прямым углам. Значит 12 углов, образованные в точках A, B и C вместе равны 12 прямым углам.
Повернём прямую AC относительно точки A (точ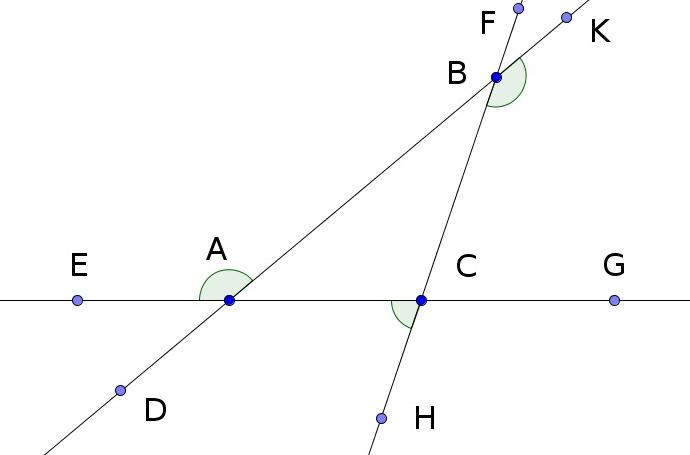
ка A остаётся на месте) по часовой стрелке, до совпадения с прямой AB. При этом прямая повернулась на угол EAB. Теперь повернём нашу прямую по часовой стрелке относительно точки B до совпадения с прямой BC. Угол поворота – KBC. Поворачиваем нашу прямую по часовой стрелке, относительно точки C, до первоначального положения AC. Угол поворота при этом – HCA. Прямая AC за три поворота совершила полный оборот по кругу. (При этом все точки на этой прямой сместились на расстояние суммы сторон треугольника, но это не имеет значения, так как в нашем треугольнике все углы и расстояния между точками сохранены). Так как прямая AC совершила полный оборот, то углы EAB, KBC и HCA вместе равны четырём прямым (Предложение 13). Так как углы через вершину равны между собой (Предложение 15), то углы DAC, ABF и BCG вместе равны четырём прямым.
У нас остались внутренние углы треугольника ABC, а именно BAC, ABC и BCA, а также равные им через вершину углы, а именно EAD, FBK и GCH. На их общую сумму остаётся 12-8=4 прямых угла. Следовательно углы BAC, ABC и BCA вместе равны двум прямым. И равные им углы EAD, FBK и GCH вместе равны двум прямым.
Мы взяли произвольный треугольник, но данное доказательство применимо к любому треугольнику. Значит, внутренние углы любого треугольника вместе равны двум прямым.
Было ли допустимо во времена Евклида такое доказательство? Ведь в те времена избегали использовать движение в доказательстве предложений. Я думаю, что допустимо. Так как движение используется только для того, чтобы определить углы между прямыми, которые дают полный оборот прямой. Этот способ ничуть не хуже метода наложения, используемого в книге Евклида.
Можно привести более короткое доказательство, используя этот метод. Я назвал его методом поворота прямой.
Доказательство 2 предложения 26А.
Возьмём произвольный треугольник ABC. Стороны треугольника непрерывно продолжим по прямой (Постулат 2). 
Повернём прямую AC против часовой стрелки, относительно точки A (точка A остаётся на месте) до совпадения с прямой AB. При этом прямая повернулась на угол CAB. Повернём нашу прямую против часовой стрелки относительно точки B до совпадения с прямой BC. Угол поворота – ABC. Поворачиваем нашу прямую против часовой стрелки относительно точки C до положения AC. Угол поворота – BCA. Наша прямая совершила половину оборота. (Если взять равносторонний треугольник, то точка A на прямой будет соответствовать точке C треугольника, а точка C прямой соответствовать точке A треугольника, то есть поменяются местами).
Так как прямая совершила половину оборота, то углы CAB, ABC и BCA вместе равны двум прямым.
Данное доказательство применимо к любому произвольному треугольнику, а значит внутренние углы любого треугольника вместе равны двум прямым.
Доказательство 2 предложения 26А более короткое, но оно не даёт нам расклад по всем углам образованным в точках A, B и C.
Можно продолжить рассуждения и рассмотреть методом поворота прямой выпуклый четырёхугольник.
Предложение 26Б. Внутренние углы выпуклого четырёхугольника вместе равны четырём прямым.
Доказательство.
Возьмём произвольный выпуклый четырёхугольник ABCD. Стороны четырёхугольника непрерывно продолжим по прямой (Постулат 2).
В точке пересечения прямых образуется четыре угла, равных вместе 4 прямым (Предложение 13). Следовательно, в точках A, B, C и D образуется по 4 угла, вместе равные четырём прямым. Значит в нашем четырёхугольнике образуется 16 углов, вместе равных 16 прямым.
Повернём прямую AD по часовой стрелке, относительно точки A (точка A остаётся на месте), до совпадения с прямой AB. Угол поворота – FAB.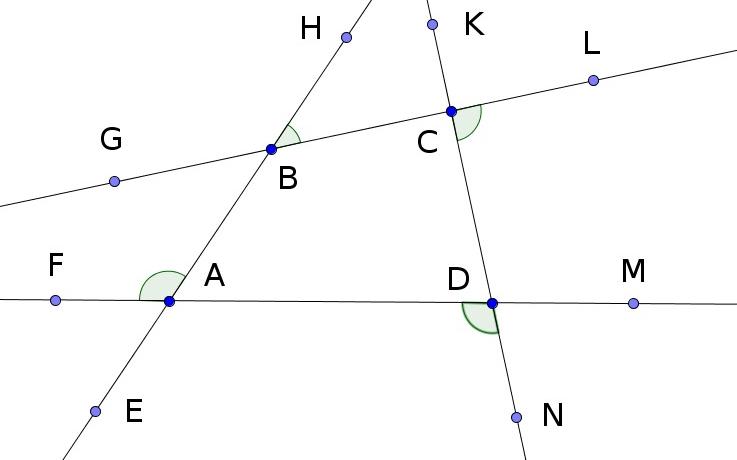 
Теперь повернём нашу прямую по часовой стрелке относительно точки B до совпадения с прямой BC. Угол поворота HBC. Поворачиваем нашу прямую по часовой стрелке относительно точки C до до совпадения с прямой CD. Угол поворота – LCD. Поворачиваем прямую по часовой стрелке относительно точки D до первоначального положения AD. Угол поворота NDA.
За четыре поворота прямая AD совершила полный оборот и вернулась на место. Значит углы FAB, HBC, LCD и NDA вместе равны четырём прямым (Предложение 13). Равные им через вершину (Предложение 15) углы EAD, GBA, BCK и CDM вместе равны четырём прямым. Углы поворота прямой и равные им через вершину, вместе равны 8 прямым.
У нас остались внутренние углы четырёхугольника ABCD, а именно – DAB, ABC, BCD и CDA, и равные им через вершину углы EAF, GBH, KCL и MDN. На их общую сумму остаётся 16-8=8 прямых.
Значит внутренние углы выпуклого четырёхугольника ABCD, а именно – DAB, ABC, BCD и CDA вместе равны 4 прямым. Равные им через вершину углы EAF, GBH, KCL и MDN вместе равны 4 прямым.
Мы взяли произвольный выпуклый четырёхугольник, но данное доказательство применимо к любому выпуклому четырёхугольнику. Значит внутренние углы любого выпуклого четырёхугольника вместе равны четырём прямым.
Следствие. Так как внутренние углы любого выпуклого четырёхугольника вместе равны четырём прямым, то существует четырёхугольник, у которого все углы прямые.
Следствие предложения 26Б является ещё одним эквивалентом 5-го постулата Евклида.
Для предложения 26Б, как и для предложения 26А возможно более короткое доказательство. Но оно даёт информацию только о внутренних углах фигуры.
Можно продолжить исследование выпуклых фигур и узнать, что сумма внутренних углов выпуклого пятиугольника равна 6-ти прямым, а выпуклого шестиугольника 8-ми прямым. Можно вывести общую формулу выпуклых фигур. Ничего нового в этом нет. Это всё давно доказано. Но традиционно, сначала доказывается сумма внутренних углов треугольника, и через это предложение доказывается всё остальное. При применении метода поворота прямой, можно исследовать суммы углов многоугольников в любой последовательности. Можно исследовать не только выпуклые многоугольники, но и любые фигуры, состоящие из прямых линий. Простота и наглядность – большой плюс этого метода. Так как прямая всегда возвращается на своё место, то она делает либо целое количество оборотов, либо с половиной. Сумма углов всегда будет кратна 4 прямым углам (целое количество оборотов), или 2 прямым (когда один поворот не полный).
Мы всё время говорили о доказательстве 5-го постулата, или его эквивалента. Но вспомним, для чего он был введён. А введён он был для доказательства предложения 29. И если доказать предложение 29 без применения 5-го постулата, то его необходимость совсем отпадает. Далее его, при желании, можно доказать в качестве предложения.
Итак, ставится новая задача: доказать предложение 29 без применения 5-го постулата. Разрешено использовать предложения с 1-го по 26-е включительно.
Приведённое доказательство предложения 29 в книге Евклида назовём доказательством 1.
Предложение 29. Прямая, падающая на параллельные прямые, образует накрестлежащие углы, равные между собой, и внешний угол, равный внутреннему, противолежащему с той же стороны, и внутренние односторонние углы, <вместе> равные двум прямым.
Доказательство 2.
Даны параллельные прямые a и b, и пересекающая их прямая c. Обозначим точку пересечения прямых a и c точкой A, а прямых b и c точкой B. Разделим отрезок AB пополам (Предложение 10). Точка C делит отрезок AB пополам. Из точки C раствором AC или CB описываем круг (Постулат 3). Необозначенные точки пересечения круга с прямыми a и b обозначим как D и E. Проводим прямую линию от точки D до точки E (Постулат 1).
Так как углы DCA и BCE равны через вершину (Предложение 15), а стороны AC, DC, BC и EC равны как раствор описанной из точки C окружности (Оп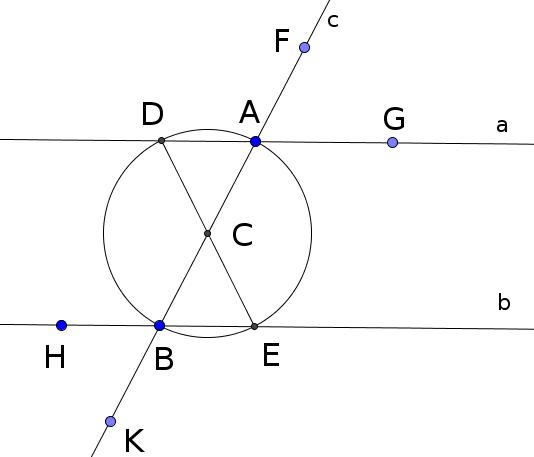
ределение 15), то треугольники DCA и BCE равны между собой (Предложение 4).
Треугольники DCA и BCE равнобедренные, так как стороны AC, DC, BC и EC равны (Определение 20). У равнобедренных треугольников углы у основания равны (Предложение 5). Следовательно, углы CDA, CAD, CBE и CEB равны. Угол DAC равен углу FAG через вершину (Предложение 15). Угол CBE равен углу HBK через вершину. Следовательно, углы FAG, DAC, CBE и HBK равны.
Так как углы FAG, DAC, CBE и HBK равны, то и дополняющие их до двух прямых углов углы (соответственно) FAD, GAC, CBH и KBE равны между собой (Предложение 13).
Так как углы DAC и CAG вместе равны двум прямым (Предложение 13), углы CBE и CBH равны двум прямым (Предложение 13), а углы DAC и CBE равны между собой и углы CAG и CBH равны между собой, то углы CAG и CBE вместе равны двум прямым, а углы DAC и CBH вместе равны двум прямым.
Следствие. Если, соединяя прямой линией точку D и точку E, прямая DE не пересекла прямую c в точке C, то прямые a и b не параллельны.
Если прямая DE не проходит через точку C, то вышеприведенное доказательство не получится. Но у нас по условию предложения 29 прямые a и b параллельны, и доказательство в силе.
09.16г – 25.02.17г.
Может возникнуть возражение: независимость 5-го постулата от других постулатов Евклида давно доказана. Следовательно доказать 5-й постулат или его эквивалент невозможно. Рассуждения на эту тему в следующем материале:
Приложение 1 Скачать 5-й постулат Математика Главная страница