Независимость 5-го постулата Евклида

 

Независимость 5-го постулата Евклида (или аксиомы параллельности, в системах аксиом других авторов) считается строго доказанной. То есть её в принципе нельзя доказать с помощью других аксиом или постулатов.

Аксиома считается независимой, если она не может быть получена как следствие остальных аксиом. Обычный приём доказательства независимости той или иной аксиомы a заключается в том, что строят реализацию (модель) системы аксиом без аксиомы a, в которой аксиома a не выполняется. Если такую реализацию удаётся построить, то аксиома a независима.

Действительно, если бы a получалась как следствие остальных аксиом, то в реализации (модели) также было бы справедливо утверждение a, но это противоречит построению модели (реализации). (Смотри Погорелов А.В. Основания геометрии 1979г. стр.63).

Самыми известными моделями, которые самим своим существованием доказывают независимость 5-го постулата Евклида (аксиомы параллельности) являются модель Пуанкаре и модель Клейна.

Модель Пуанкаре существует в двух разновидностях – в окружности и на полуплоскости. Для полуплоскости роль прямых выполняют содержащиеся в ней полуокружности, с центрами на ограничивающей её прямой и лучи перпендикулярные этой прямой.

 

 

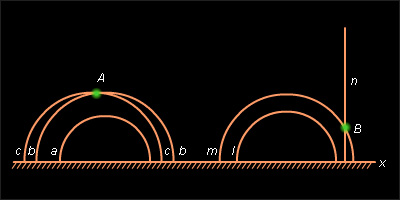
Для модели Пуанкаре в окружности, за плоскость принимают внутренность круга. Роль прямых выполняют содержащиеся в этом круге дуги окружностей и его диаметры.

 

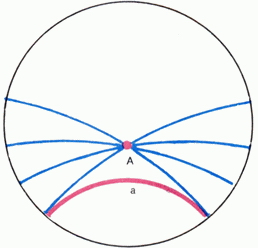
В модели Пуанкаре пятый постулат Евклида не выполняется.

Модель Клейна представляет собой внутренность окружности. Роль прямых выполняют хорды внутри круга.

 

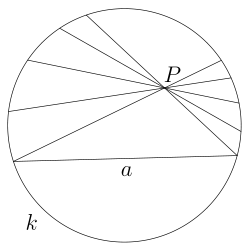
В модели Клейна пятый постулат Евклида не выполняется.

Модель Клейна использует Погорелов А.В. (Основания геометрии 1979г. стр. 65-68) для доказательства независимости 5-го постулата.

Давайте подробнее рассмотрим модель Клейна. Действительно ли в ней выполняются все аксиомы, кроме аксиомы параллельности?

 
Если модель Клейна рассмотреть в аксиоматике Евклида, то в ней, кроме 5-го постулата, не выполняется:

1. 2-й постулат. И что ограниченную прямую <можно> непрерывно продолжать по прямой.

2. 3-й постулат. И что из всякого центра и всяким раствором <может быть> описан круг.

 

Кроме того, в этой модели, по определению, не может быть параллельных.

Определение: Параллельные суть прямые, которые, находясь в одной плоскости и будучи продолжены в обе стороны неограниченно, ни с той ни с другой <стороны> между собой не встречаются..

В модели Клейна, применяя аксиоматику Евклида, не все аксиомы выполняются. Следовательно независимость 5-го постулата не доказана.

Рассмотрим модель Клейна в аксиоматике Гильберта. Кроме аксиомы параллельности в ней не выполняются:

1. Аксиома порядка 2.2. Если A и C – точки одной прямой, то существует по меньшей мере одна точка B, лежащая между A и C, и по меньшей мере одна точка D, такая, что C лежит между A и D.

Если принять за точку C один из концов хорды (прямой в модели Клейна), то точка D не существует.

 

2.. Аксиома конгруэнтности 3.1. Если A,B две точки на прямой a, а A₁ точка на той же прямой или на другой прямой a₁, то всегда можно найти по данную от точки A₁ сторону прямой a₁ одну и только одну такую точку B₁, что отрезок AB конгруэнтен, или равен отрезку A₁B₁.

Мы говорим также короче: каждый отрезок может быть однозначно определённым образом отложен по данную сторону на данной прямой от данной точки.

Эта аксиома не всегда выполняется в модели Клейна, так как точка B₁ может выйти за границу окружности, и тогда она не существует, и отложить отрезок выходящий за пределы модели мы не сможем. А по аксиоме точку можно найти всегда, и отрезок отложить можно всегда.

 

3. Аксиома непрерывности 5.1. (Аксиома измерения или аксиома Архимеда) Пусть A₁ есть произвольная точка на прямой между произвольно данными точками A и B; строим затем точки A₂, A₃, A₄,… так, что точка A₁ лежит между A и A₂, A₂ между A₁ и A₃, A₃ между A₂ и A₄ и т.д., и сверх того отрезки AA₁, A₁A₂, A₂A₃, A₃A₄, … равны между собою: тогда в ряду точек A₂, A₃, A₄,… всегда существует такая точка A_n, что точка B лежит между A и A_n.

 

Если за точку B (по аксиоме можно выбирать произвольно) взять последнюю точку хорды (прямой в модели Клейна) с любой стороны, то точка A_n выходит за границу модели, а значит, она не существует. По аксиоме точка A_n существует всегда.

 
Аксиомы Гильберта взяты из издания 1923г. под редакцией Васильева А.В., перевод с 5-го немецкого издания.

В книге Гильберта «Основания геометрии» изданного в 1948г. под редакцией Рашевского П.К., перевод с 7-го немецкого издания, аксиомы переформулированы и изменены. Из аксиомы порядка 2.2 исчезает точка D. И тогда в модели Клейна аксиома выполняется всегда. Аксиомы 3.1 и 5.1 хоть и изменены, но в модели Клейна не выполняются, как и в издании 1923г.

В модели Клейна, при применении аксиоматики Гильберта, некоторые аксиомы выполняются не всегда, следовательно независимость 5-го постулата не доказана.

 

Если рассмотреть модель Клейна в системе аксиом, применяемых Погореловым, то кроме аксиомы параллельности в ней не выполняется одна аксиома порядка.

Аксиома 2.4. В одном из двух направлений для каждой точки B найдутся точки A и C такие, что A предшествует B, а B предшествует C.

 

Если за точку B взять последнюю точку хорды (прямой в модели Клейна), то мы не найдём точку A или точку C (в зависимости от того какой край хорды мы выбрали для точки B). Эта точка выходит за границу модели, и поэтому её не существует. А по аксиоме она должна найтись всегда.

Так как аксиома не всегда выполняется в модели Клейна, то независимость аксиомы параллельности, при применении системы аксиом Погорелова не доказана.

 
У Евклида неограниченность плоскости прямо указана в 3-х аксиомах и определении. И если мы меняем или исключаем 5-й постулат, то плоскость всё равно остаётся явно неограниченной. Выводы полученные в модели Клейна, в модели Пуанкаре или в любой другой модели, имеющей границу, неприменимы к неограниченной плоскости.

 
У Гильберта неограниченность плоскости прямо не указывается. Но несколько аксиом косвенно это подтверждают. Эти аксиомы в модели Клейна (или в любой модели имеющей границу), в зависимости от выбора точек могут выполняться, а могут и нет. Достаточно одной ситуации, когда аксиома не выполняется в модели, чтобы признать аксиому невыполнимой. И поэтому модель Клейна в аксиоматике Гильберта ничего не доказывает для неограниченной плоскости.

 

Все возможные системы аксиом можно свести к трём видам:

1. Неограниченность плоскости явно указывается аксиомой параллельности, и ещё хотя бы одной аксиомой. (Пример – аксиоматика Евклида).

2. Неограниченность плоскости явно не указывается. Но косвенно подтверждается в аксиоме параллельности и ещё хотя бы одной аксиомой. (Пример – аксиоматика Гильберта, Погорелова).

3. Неограниченность плоскости явно или косвенно подтверждается только аксиомой параллельности. И если мы её исключаем (или изменяем), то уже не можем отличить неограниченную плоскость от её части, имеющую границу. И выводы полученные при исключении аксиомы параллельности нельзя переносить на неограниченную плоскость.

 

Независимость 5-го постулата Евклида на неограниченной плоскости не доказана. Для такого доказательства модель (реализация) не должна иметь границ.

Так как независимость 5-го постулата не доказана, то доказательство 5-го постулата возможна. Я предлагаю такое.

 

https://massenerg.kz/5-postulat-evklida.html

 

 

Литература:

Евклид Начала. Перевод с греческого А.Д.Мордухай-Болтовского 1948г

Гильберт. Основания геометрии под редакцией Васильева А.В. перевод с 5-го немецкого издания 1923г

Гильберт. Основания геометрии под редакцией Рашевского П.К. перевод с 7-го немецкого издания 1948г

Погорелов А.В. Основания геометрии 1979г

 

04.2017г-24.03.2018г

Опубликовано 28.03.2021г

 

 

 Главная            Математика           5-й постулат Евклида