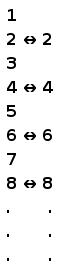Масса и энергия
Счётно ли бесконечное множество вещественных чисел?
Можно ли объединить в пары бесконечное множество вещественных чисел и бесконечное множество натуральных чисел? Считается, что это невозможно. Даже в промежутке между 0 и 1 вещественных чисел больше, чем натуральных чисел в бесконечном множестве натуральных чисел. Так как невозможно составить взаимно – однозначное соответствие между вещественными числами этого промежутка и натуральными числами. Чтобы каждому вещественному числу сопоставлялось одно и только одно число натуральное. Попробуем осуществить такое сопоставление.
Натуральные числа можно располагать по порядку: 1, 2, 3, 4, 5 и т.д. Вещественные числа так выстроить нельзя. Во множество вещественных чисел входят как рациональные, так и иррациональные числа. Иррациональные числа имеют бесконечное количество знаков после запятой. Поэтому бесконечное множество вещественных чисел, обычно объединяют в матрицу, у которой числа вниз и цифры вправо уходят в бесконечность. Каждой строке соответствует одно вещественное число. Например:
Нам необходимо сформировать правило взаимно – однозначного сопоставления вещественных чисел промежутка 0 – 1, и натуральных чисел. Таких правил сопоставления можно составить бесконечно много. Но мы возьмём одно простое правило, чтобы у нас получилась симметрия сопоставляемых множеств.
Итак, правило сопоставления вещественных чисел промежутка 0 – 1 и натуральных чисел: В каждой паре чисел, первому знаку после запятой у вещественного числа соответствует цифра единиц числа натурального, второму – цифра десятков, третьему цифра сотен, четвёртому цифра тысяч и т.д.
Цифры у вещественных и натуральных чисел будут соответствовать:
1 → 1, 2 → 2, 3 → 3, 4 → 4, 5 → 5, 6 → 6, 7 → 7, 8 → 8, 9 → 9, 0 → 0.
Согласно этому простому правилу, у нас получается зеркальное расположение цифр в паре вещественное число – число натуральное.
Для полной симметрии матрицу можно представить так:
В актуальной бесконечности, каждому вещественному числу промежутка 0 – 1 будет соответствовать одно и только одно натуральное число. Значит мощность бесконечного множества вещественных чисел промежутка 0 – 1 и бесконечного множества натуральных чисел одинакова.
Какие могут возникнуть возражения?
1. А почему натуральные числа расположены не по порядку?
Обычно натуральные числа располагают в ряд 1, 2, 3, 4, 5 и т.д., потому что есть такая возможность. Но если мы поменяем порядок расположения? От этого, что измениться количество натуральных чисел? Если бы это было так, то уже давно изучали отличительные свойства рядов натуральных чисел, расположенных в различном порядке.
Матрица у нас симметричная, и поэтому можно задать встречный вопрос: почему во всех доказательствах превосходящей мощности вещественных чисел, в матрице вещественные числа расположены не по порядку? Как только вещественные числа будут расположены по возрастанию или убыванию, не составит труда объединить их в пары с натуральными числами.
2. Применяя диагональный процесс, методом от противного, можно доказать несчётность вещественных чисел.
Правило применённое в этом диагональном процессе: если по диагонали цифра 1, то в числе, не входящем в перечень пишем 9, во всех других случаях пишем 1.
Матрица сопоставления вещественных чисел промежутка 0 – 1 и натуральных чисел у нас симметричная, поэтому диагональный процесс можно провести, по этому же правилу, и в части натуральных чисел. И получить натуральное число соответствующее вещественному числу, не вошедшему в рассматриваемый фрагмент бесконечной матрицы.
О чём говорит нахождение числа, не входящего в рассматриваемый фрагмент матрицы? Только о том, что его нет в рассматриваемом фрагменте. Но во всей бесконечной матрице оно есть, и есть соответствующая пара вещественное число – число натуральное. (Почему всё-таки можно найти число не входящее в рассматриваемый фрагмент бесконечной матрицы рассмотрено в статье «Корректен ли диагональный метод?». Ответу на этот вопрос посвещено не мало мест в альманахе MOI в материалах Валдиса Валевича Эгле и Марины Олеговны Ипатьевой).
3. Натуральные числа всегда конечные, а в матрице это не видно. Бывают ли такие большие натуральные числа, состоящие из бесконечной последовательности цифр, уходящей влево?
Можно ответить встречным предложением – назовите самое большое натуральное число, больше которого нет натуральных чисел.
Почему для иррациональных чисел, бесконечная последовательность цифр после запятой вправо считается нормальным явлением, а для натуральных чисел, бесконечная последовательность цифр до запятой влево вызывает вопросы? Ведь множество натуральных чисел бесконечно.
Мы взаимно – однозначно сопоставляли натуральные числа и вещественные числа промежутка 0 – 1. При этом у нас каждому вещественному числу этого промежутка соответствовало одно и только одно натуральное число. Лишних натуральных чисел у нас не осталось. Но таких промежутков во множестве всех вещественных чисел бесконечное множество. Значит ли это – что нельзя взаимно - однозначно сопоставить вещественные числа и числа натуральные? И что мощность бесконечного множества вещественных чисел больше мощности множества натуральных чисел? Больше ли количество вещественных чисел количества натуральных чисел?
Попробуем получить взаимно – однозначное соответствие между вещественными числами и числами натуральными. Запятая, у вещественных чисел может располагаться в любом месте. Возьмём такой пример фрагмента матрицы вещественных чисел:
Правило для сопоставления вещественных чисел промежутка 0 – 1 и натуральных чисел, которое мы применяли выше, не подходит. Так как запятая, отделяющая целую часть вещественного числа, может находиться где угодно. И поэтому, необходимо создать новое правило (таких правил сопоставления можно создать бесконечное количество).
Правило взаимно – однозначного сопоставления вещественных чисел и натуральных чисел:
В каждой паре чисел первой цифре вещественного числа соответствует цифра единиц числа натурального, второй цифре – цифра сотен, третей – цифра десятков тысяч и т.д.
Чётные цифры (справа на лево) у натуральных чисел зарезервируем для запятой у чисел вещественных. Если есть запятая, то ставим единицу, если нет, то 0.
Цифры у вещественных и натуральных чисел будут соответствовать:
1 → 1, 2 → 2, 3 → 3, 4 → 4, 5 → 5, 6 → 6, 7 → 7, 8 → 8, 9 → 9, 0 → 0.
По нашему правилу, при каждом шаге рассматриваемого фрагмента матрицы – часть матрицы с натуральными числами будет расширяться влево вдвое быстрее, чем правая часть с вещественными числами. Так как на каждую цифру вещественного числа приходится две цифры числа натурального. Правая цифра сопоставляется цифре вещественного числа, левая описывает, есть ли после этой цифры у вещественного числа запятая.
Такое сопоставление ничуть не хуже взаимно – однозначного сопоставления чётных и натуральных чисел. При переходе к актуальной бесконечности, матрица у нас бесконечна вправо, влево и вниз.
Пример фрагмента нашей матрицы:
Каждому вещественному числу соответствует одно и только одно число натуральное. В каждом вещественном числе есть только одна запятая, отделяющая целую часть числа. По нашему правилу мы зарезервировали бесконечное число цифр, для отображения запятой. Бесконечное количество натуральных чисел не участвует в нашем взаимно-однозначном соответствии. Однако на каждое вещественное число есть число натуральное. Значит ли это – что мощность бесконечного множества натуральных чисел больше мощности бесконечного множества всех вещественных чисел? Составляя взаимно – однозначное соответствие натуральных и вещественных чисел промежутка 0 – 1, мы получили, что их одинаковое количество, и «лишних» натуральных чисел нет. Нет ли тут противоречия?
Противоречия нет, если мы примем, что «мощность» сравниваемых бесконечных множеств, не имеет отношения к самим бесконечным множествам, а относится к правилам сопоставления. Какие мы примем правила – такой результат и получим.
И поэтому я считаю, что сравнение мощностей бесконечных множеств есть занятие пустое и бесперспективное, так как к самим бесконечным множествам это сравнение не имеет никакого отношения.
Рассмотрим совсем простой пример. Сравним мощность бесконечного множества натуральных чисел и бесконечного множества чётных чисел. Мы можем принять различные правила сопоставления наших множеств. Например, сопоставим по порядку натуральные и чётные числа:
Каждому натуральному числу соответствует одно и только одно чётное число. Так как множества у нас бесконечные, то при переходе к актуальной бесконечности каждому натуральному числу соответствует чётное число. Значит мощность множеств у нас одинаковая.
Теперь изменим правила. Каждому числу бесконечного множества чётных чисел сопоставим чётные числа из множества натуральных чисел:
Каждому числу бесконечного множества чётных чисел соответствует одно и только одно число из бесконечного множества чисел натуральных. А у бесконечного множества натуральных чисел половина чисел осталось без пары. Значит ли это – что натуральных чисел вдвое больше?
Изменяя правила сопоставления, мы можем получить какой угодно результат. Что натуральных чисел у нас втрое, в вчетверо и т.д. больше чем чётных чисел. А можем получить, что чётных чисел больше, чем натуральных в любое количество раз. Всё зависит от правил взаимно – однозначного сопоставления. К самим бесконечным множествам это не имеет ни какого отношения. Понятие «счётность» бесконечного множества, как и понятие «мощность» бесконечного множества к бесконечным множествам неприменимо.
14.01-29.01.17г.